Quem sabe se ligar de um modo diferente você consiga conectar as 3 companhias nas 3 casas?
Depois de tentar por muitas e muitas vezes unir as 3 casinhas com Água, Luz e Esgoto, ouvi que era impossível. Mas acreditei parcialmente…
Passavam-se os anos, e de vez em quando eu pegava este desafio para tentar resolver, pensando de formas diferentes, tentando estratégias diferentes… Mas nunca chegando a uma solução.
No começo de 2011 estava em meu quinto semestre de graduação em Matemática, quando conheci um professor pra lá de peculiar. Ele se apresentava como E.T. (as abreviações de seu nome), e suas aulas de Cálculo III eram estranhamente dinâmicas, bem humoradas e interativas. Meu trajeto até este semestre tinha sido bastante turbulento, muitas reprovações, dúvida constante sobre se eu estava no curso certo, se deveria ou não continuar, ao mesmo tempo que tinha um grande prazer por tudo aquilo que acontecia nas aulas, ainda que não conseguisse corresponder.
Em meio a essas aulas, veio a notícia de que estaria começando naquele semestre um evento todas as sextas-feiras, chamado Seminários de Coisas Legais e ocorreria às 13h13. O professor convidava a toda a turma para quem quisesse compor as apresentações, bastava entrar em contato, a única condição é que o tópico apresentado deveria “ser legal”.
Assistindo as apresentações ficava claro que eram realmente seminários legais, e dava vontade de apresentar também. Mas o que eu poderia levar de legal, se mal conseguia o 5.0 necessário pra passar nas disciplinas? Então veio a memória daquele desafio de ligar as 3 casinhas com Água, Luz e Esgoto. Entrei em contato com o professor e apresentei o problema, ele achou legal o suficiente para expor, mas queria ver o que eu faria antes de marcar a apresentação.
Pesquisei bastante, em blogs, sites, e vários lugares e tentei escrever em matematiquês até formar um “argumento” que garantisse o problema não ter solução. Fiz várias análises, tentei reescrevê-lo de diferentes maneiras utilizando toda aquela matemática que conhecia, usei muitas imagens, e cheguei a um argumento que me convencia de realmente não ter solução. Estava perfeito aos meus olhos, até levar aos professores que estariam me auxiliando naquele momento, e descobri que minha demonstração não demonstrava nada XD. Era algo empírico, mostrava para alguns casos, mas nem de longe garantiria a abrangencia daquele resultado. Hoje analisando, realmente eu não poderia ter chegado naquela demonstração sozinha, já que faltavam algumas ferramentas que estavam para além do repertório conhecido de geometria.
Enfim, com a orientação deles vim a aprender uma propriedade nova de geometria, um resultado que garantiria realmente não ter solução para este problema. Admito que precisei ler umas 20 vezes essa propriedade, fazer rascunhos com valores, testes e tudo mais pra começar a entender mais ou menos o que ela dizia. Mas a parte legal é que estava satisfatória para apresentar.
Então essa jovem, com seus 19 anos, que até então teve um trajeto acadêmico de muitos tropeços e quedas nas disciplinas mais básicas do curso, ganha seu momento de palestrar.
No dia fui de bicicleta para o campus, embaixo de uma chuva torrencial. Cheguei mais molhada do que se tivesse pulado numa piscina, e me sequei com papel toalha no banheiro uns 20 minutos antes de começar. Nervosismo, ansiedade, uma platéia que já seria intimidadora para uma aluna mediano, estava agora em silêncio para me ouvir falar de algo que eu segurava com dificuldade.
Essa foi uma experiência que realmente me influenciou positivamente. Minha primeira palestra. Minha primeira apresentação de um tópico de matemática para o público acadêmico (fora as atividades dentro de disciplinas). Mas foi um momento que recebi coragem e apoio de vários professores, em particular deste que se apresentava como E.T. Depois disso tive uma maior segurança e estímulo para apresentar em outros lugares, para falar de matemática e me arriscar em aprender propriedades apenas por achá-las legais. Tanto que 12 anos depois estou aqui escrevendo sobre esta experiência.
E então… cade a demonstração?
Vamos lá, para a parte 3 deste texto, pois a demonstração merece todo um desenvolvimento cuidadoso.
Trabalhar em cima desta demonstração, de certa forma, me incentivou a pesquisar e estudar matemática de forma séria e divertida.
Vamos começar!
Primeiramente devemos olhar nosso problema como uma questão de grafos no plano bidimensional:
Cada casa ou companhia equivale a um vértice, ou seja, uma unidade pontual;

Para facilitar a notação, vou redesenhá-los como pontinhos no plano, denotados por B (casa azul), Y (casa amarela), R (casa vermelha), G (companhia de água), C (companhia de luz) e P (companhia de esgoto).

Vamos definir também que toda conexão entre uma casa e uma empresa será chamada de aresta.
Mas não necessariamente estas arestas precisam ser segmentos de retas (basta que seja uma linha que comece e termine em vértices e não se cruze com nenhuma outra linha). Exemplo de duas arestas G-B e G-Y.

Por fim, cada região do plano, totalmente cercada por arestas, será chamada de uma face. Por exemplo, se eu inserir as arestas C-B e C-Y, formamos duas faces cercada pelos vértices G, C, B e Y (sim, são duas faces, a interna em laranja e a externa que representa o restante do plano).

Assim, temos 6 arestas (B, Y, R, G, C e P) e seeeeeeeeeeeeeeeeeeeeeeeeeee o problema tiver solução, então ele deverá ter 9 arestas:
- G-B, G-Y, G-R
- C-B, C-Y, C-R
- P-B, P-Y, P-R
Então, se sabemos o número de vértices e de arestas, podemos usar a fórmula de Euler para determinar o número de faces (eu falo um pouco sobre a fórmula de Euler no contexto tridimensional neste texto O Garlon faz vários cortes no poliedro, mas a fórmula de Euler é implacável).
Para o plano: (número de faces) + (número de vértices) – (número de arestas) = 2
(número de faces) + 6 – 9 = 2
(número de faces) = 5
Assim, seeeeeeeeeeeeeeeeeeeeeeeee houver solução, teremos 5 faces, 9 arestas e 6 vértices.
Vamos agora analisar como será a relação destas 5 faces com nossas 9 arestas.
Faces formadas por 1 aresta (chamaremos de Faces-1): besteira! Pois teríamos um vértice ligado a ele mesmo com uma mesma aresta. Veja que na figura abaixo temos duas faces foramadas pela aresta G-G, a face interna e a face externa.

Faces formadas por 2 arestas (chamaremos de Faces-2): estranho! Pois estamos fazendo ligando duas vezes uma mesma companhia de uma casa. Veja que na figura abaixo temos duas faces foramadas por duas arestas G-B e B-G, a face interna e a face externa.

Faces formadas por quantidades ímpares de arestas: sem sentido… pois teríamos uma ligação entre duas casas, ou entre duas companhias (o famoso “gato”). Veja que na figura abaixo temos duas faces foramadas por três arestas G-B, B-C, G-C, a face interna e a face externa.

Veja que na figura abaixo temos duas faces foramadas por cinco arestas B-Y, Y-P, P-R, R-C, C-B, a face interna e a face externa.

Com isso, as faces da nossa solução devem ser formadas por um número par de arestas, maior ou igual a 4.
No entanto, existe um teorema matemático válido para grafos no plano, que diz:
2*(número de arestas) = 1*Face-1 + 2*Face-2 + 3*Face-3 + 4*Face-4 + 5*Face-5 + 6*Face-6 + …
onde Face-N representa o número de faces formadas por N arestas.
Agora combinando o resultado da fórmula de Euler, de quando supomos que o problema teria solução, com este novo teorema, temos que:
2*9 = 1*Face-1 + 2*Face-2 + 3*Face-3 + 4*Face-4 + 5*Face-5 + 6*Face-6 + …
Mas como vimos antes, faces com 1 aresta, 2 arestas e qualquer quantidade ímpar de arestas, não faz sentido para nossa solução. Então temos:
18 = 1*0 + 2*0 + 3*0 + 4*Face-4 + 5*0 + 6*Face-6 + 7*0 + 8*Face-8 + …
Simplificando fica:
18 = 4*Face-4 + 6*Face-6 + 8*Face-8 + …
Mas observe que pela fórmula de Euler, eu tenho 5 faces, então:
Face-4 + Face-6 + Face-8 + Face-10 + Face-12 + … = 5
Ou seja,
18 = 4*Face-4 + 6*Face-6 + 8*Face-8 + 10*Face-10 + 12*Face-12 … ≥ 4*5 + 6*0 + 8*0 + 10*0 + 12*0 + …
Concluímos com isso que:
18 ≥ 20
Mas isso é um absurdo!
Logo, como consequência temos que aquela hipótese inicial de que o problema teria solução no plano, é falsa.












 A brancura do ambiente era total. Alguns pontos escuros na paisagem eram a exceção. Trenós mecanizados e também os puxados com cachorros cortando o gelo eram pontos atravessando a meseta central da Groenlândia. Dois riscos pretos bem pequenos apareceram ao fundo no horizonte. Ao chegar mais perto, os homens dos trenós viram que eram dois esquis num montículo de neve. Ao escavar o montículo, surgiu o cadáver que eles tanto procuravam e não queriam encontrar. As buscas acabaram. Alfred Wegener, o chefe daquela expedição e um dos maiores cientistas do século, estava oficialmente morto.
A brancura do ambiente era total. Alguns pontos escuros na paisagem eram a exceção. Trenós mecanizados e também os puxados com cachorros cortando o gelo eram pontos atravessando a meseta central da Groenlândia. Dois riscos pretos bem pequenos apareceram ao fundo no horizonte. Ao chegar mais perto, os homens dos trenós viram que eram dois esquis num montículo de neve. Ao escavar o montículo, surgiu o cadáver que eles tanto procuravam e não queriam encontrar. As buscas acabaram. Alfred Wegener, o chefe daquela expedição e um dos maiores cientistas do século, estava oficialmente morto.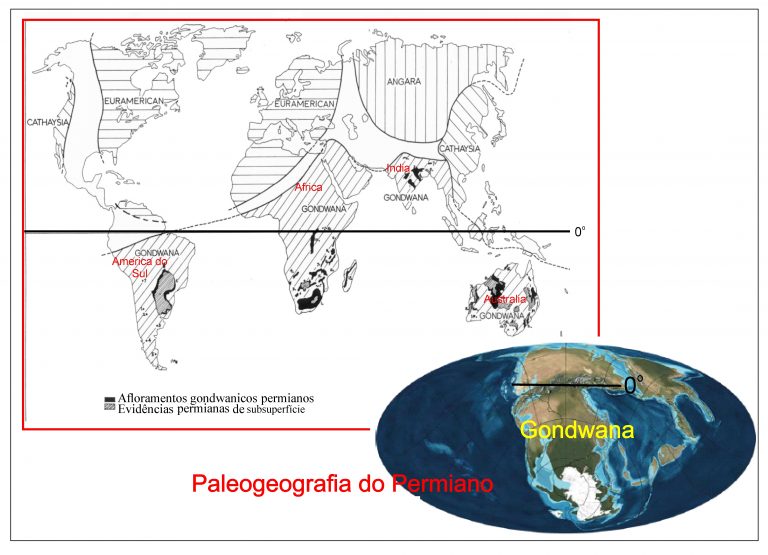

 Sob a denominação de Flora de Glossopteris, ou Província Florística do Gondwana, são reunidos todos os registros de plantas, sejam eles folhas, caules, sementes, lenhos, pólens, charcoals, etc. que apresentam similitudes morfológicas e aparecem no meio das rochas sedimentares de idade permiana (298 – 252 Ma) que são encontradas na porção sul da África e América do Sul, bem como na Austrália, Antartica, Nova Zelândia e a Índia. Todos esses continentes hoje se encontram separados por oceanos, mas durante muitos milhões de anos, aproximadamente de 500 até 160 Ma ficaram unidos formando um grande paleocontinente denominado como Gondwana. O nome foi inspirado no local da India onde os primeiros indícios do paleocontinente foram encontrados, entre eles a Flora de Glossopteris.
Sob a denominação de Flora de Glossopteris, ou Província Florística do Gondwana, são reunidos todos os registros de plantas, sejam eles folhas, caules, sementes, lenhos, pólens, charcoals, etc. que apresentam similitudes morfológicas e aparecem no meio das rochas sedimentares de idade permiana (298 – 252 Ma) que são encontradas na porção sul da África e América do Sul, bem como na Austrália, Antartica, Nova Zelândia e a Índia. Todos esses continentes hoje se encontram separados por oceanos, mas durante muitos milhões de anos, aproximadamente de 500 até 160 Ma ficaram unidos formando um grande paleocontinente denominado como Gondwana. O nome foi inspirado no local da India onde os primeiros indícios do paleocontinente foram encontrados, entre eles a Flora de Glossopteris.

 Como amante da paleontologia e, mais recentemente, praticante e apreciadora de wushu, a inspiração deste post surgiu como um desafio de tentar relacionar os dois temas de alguma forma. Me parece que alguns mitos são criados a partir de “verdades”…distorcidas, ou, com um toque de imaginação, digamos assim. Na arte marcial que conhecemos por “kung fu”, aqui no ocidente, existem diversos estilos de luta. Norte e Sul da China são conhecidos por estilos diferentes. O estilo do dragão é um estilo imitativo do Sul; neste, os movimentos devem ser compreendidos, internalizados (em contraposição, o adversário do dragão é o tigre e seu estilo é fundamentado em movimentos de força e memorização).
Como amante da paleontologia e, mais recentemente, praticante e apreciadora de wushu, a inspiração deste post surgiu como um desafio de tentar relacionar os dois temas de alguma forma. Me parece que alguns mitos são criados a partir de “verdades”…distorcidas, ou, com um toque de imaginação, digamos assim. Na arte marcial que conhecemos por “kung fu”, aqui no ocidente, existem diversos estilos de luta. Norte e Sul da China são conhecidos por estilos diferentes. O estilo do dragão é um estilo imitativo do Sul; neste, os movimentos devem ser compreendidos, internalizados (em contraposição, o adversário do dragão é o tigre e seu estilo é fundamentado em movimentos de força e memorização).